If one wants to describe the perpetual movement of the earth around the sun to generate solar trajectories several factors must be taken into consideration:
- Gravitational forces between planets, asteroids, moons and stars
- Earth's Axial Tilt
- ...
This many-body problem cannot be solved analytically and therefore mathematical models have been developed by fitting measured data. These models take
time, date, longitude and latitude as input parameters and return the calculated sun positions, i.e., the
elevation angle and
azimuth. Usually the elevation angle is measured from a horizontal plane (horizon) upwards. For example an elevation angle of 90° means that the position of the sun is directly above your head. The azimuth is measured from the northern direction, i.e., North corresponds to an azimuth of 0°, East to and angle of 90° and so on. With these two angles one can describe every point on a unit sphere.
The definition of the two angles may differ from model to model and should therefore be considered carefully. Also, depending on the desired accuracy (output) and time-frame (input) ond should always keep in mind, that the physical boundaries changes over time: For example the axial tilt of earth has changed over time and can change as a result of earthquakes or meteorite impacts. Subjectivity has a big impact on the calculation of times: Time, dates and calendars differ from era to era, depending on their ruler and important events which may happened during their reign.
Calculation of solar angles have been done using the model presented on the following site:
http://www.esrl.noaa.gov/gmd/grad/solcalc/calcdetails.html
The given input-date (Year, month, day, hours, minutes, seconds) the julian date (JD) is calculated. With additional information (longitude, latidude and timezone) the JD then is inserted into the fitting formula and the position of the sun (elevation, azimuth) is calculated.
The resulting data has been checked for consistency, which will be presented below.
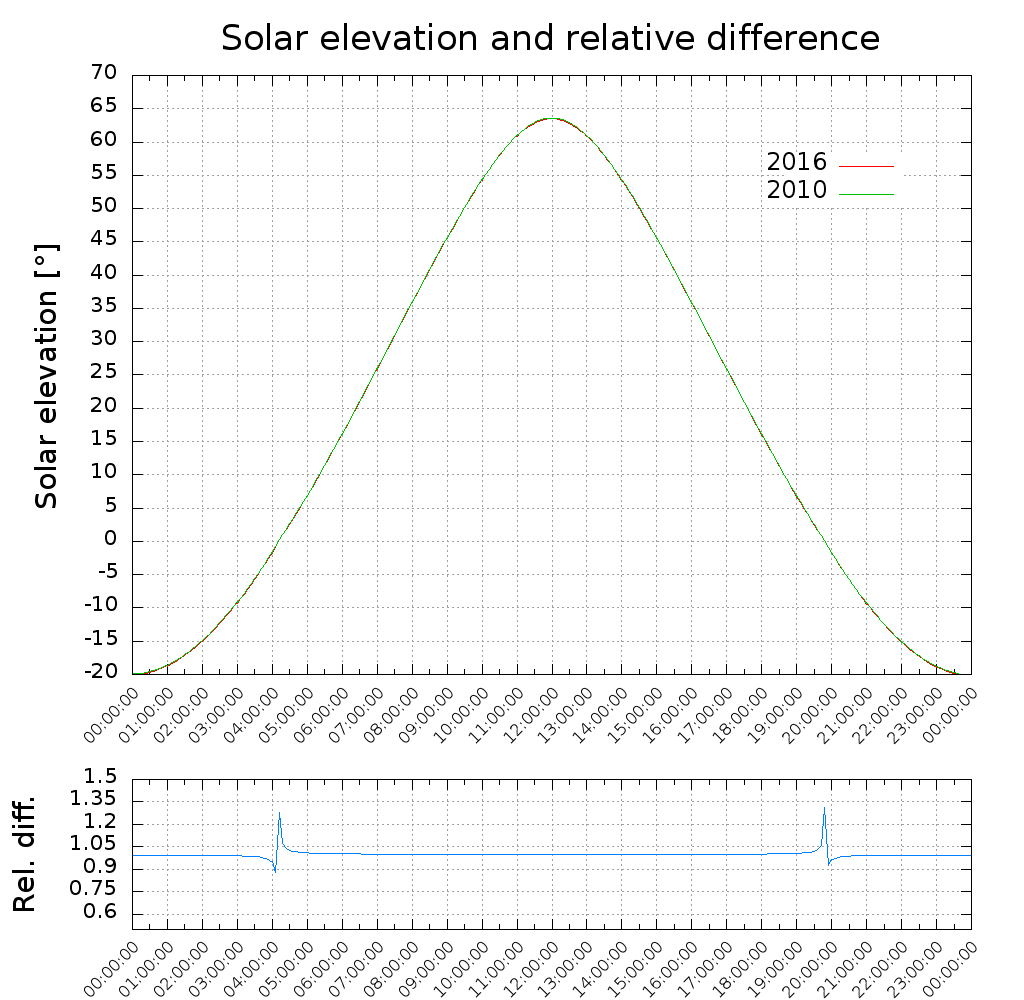
A direct comparison of two different years but the same month and day shows that the generated plots are identical. The spike in the relative difference happens due to the zero-crossing of the function, which marks dusk and dawn.
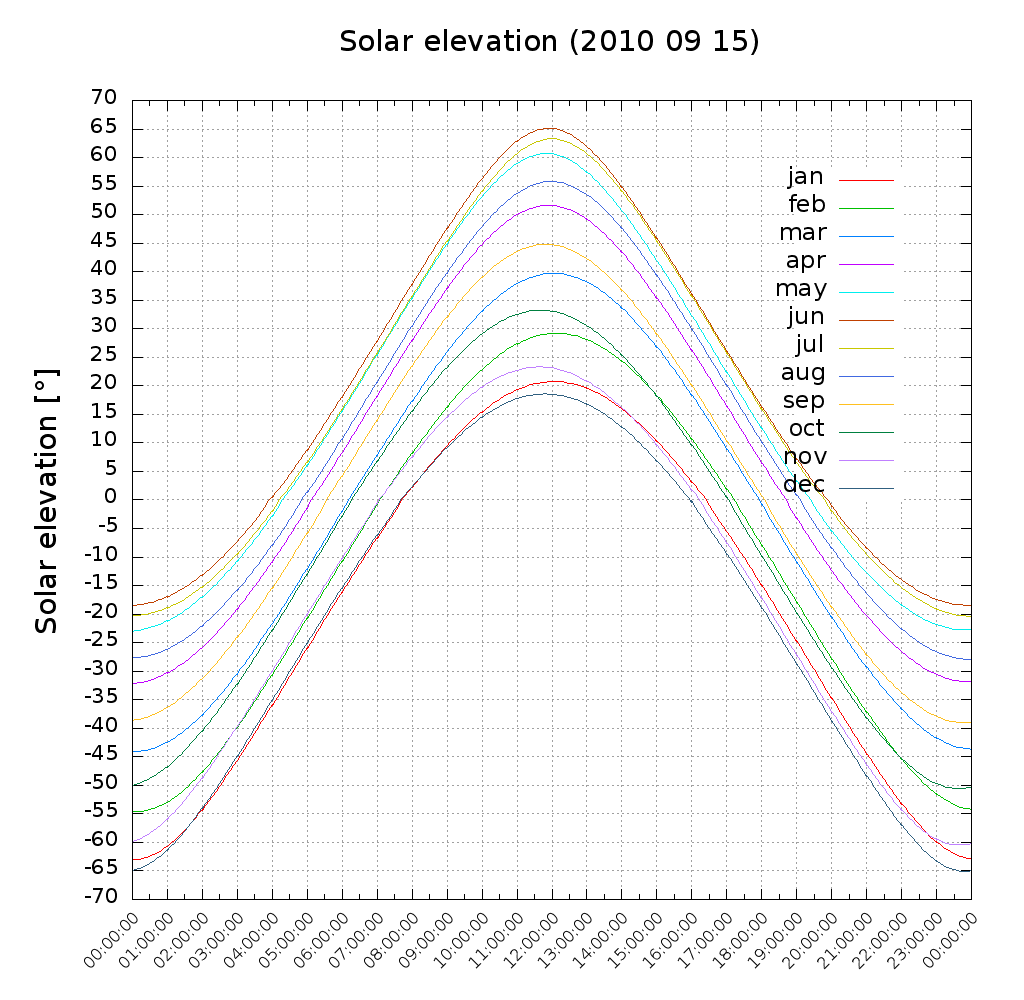
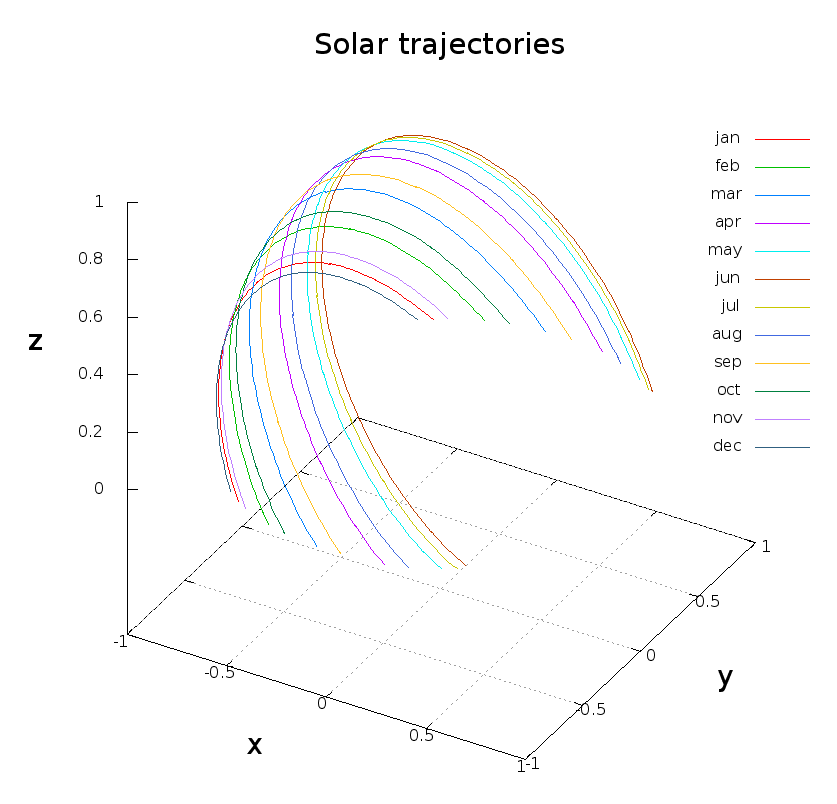
The plots for each month below: The maximum solar elevation angle (noon) increases from around january until june and decreases then. With the sun reaching greater peak heights, the duration of the day also increases.
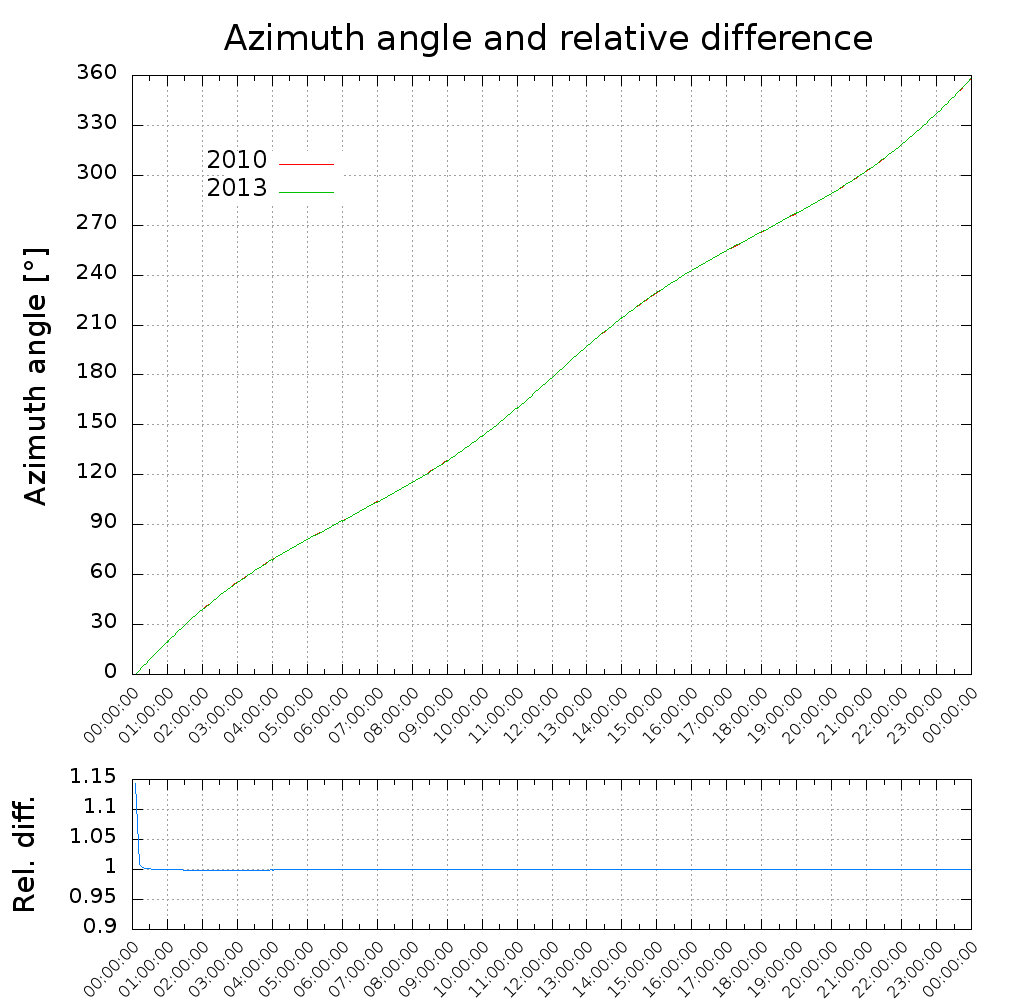
Over a day the azimuth is nearly a linear function:
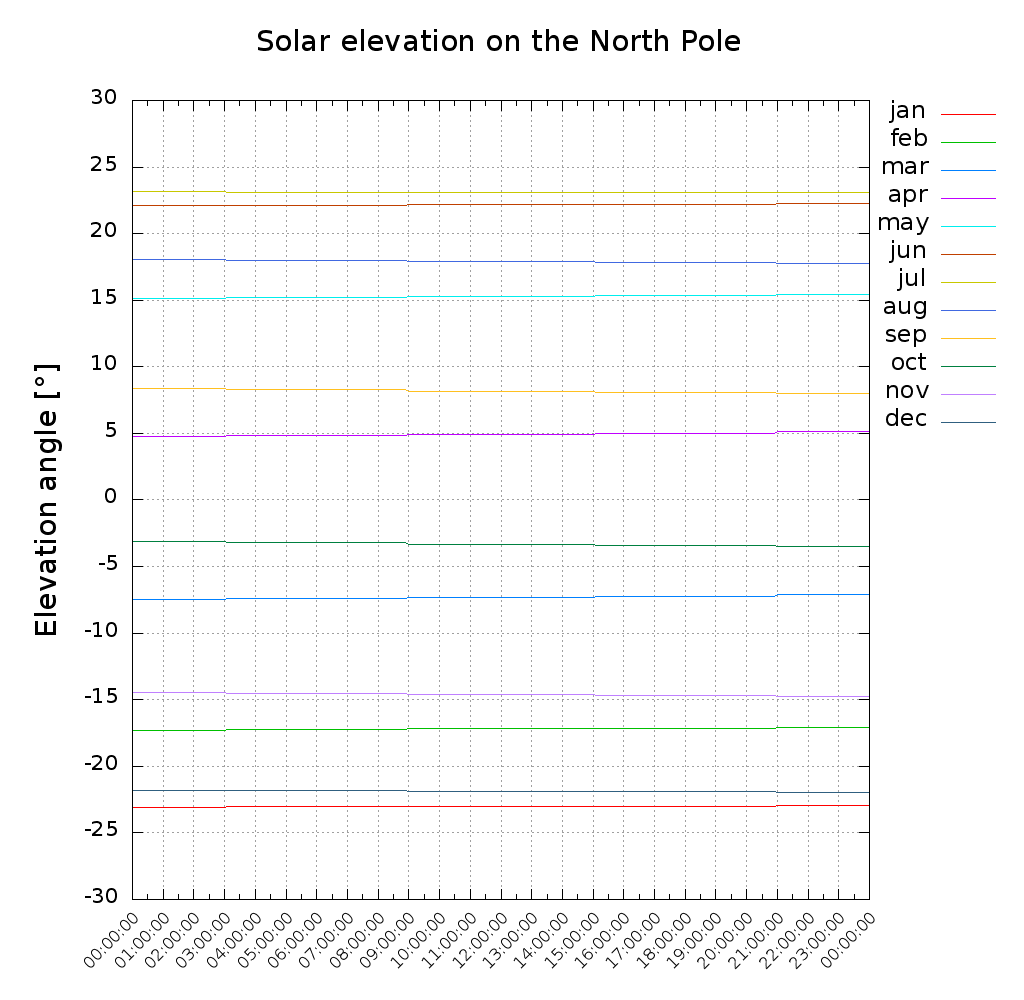
Due to the Earth's Axial Tilt there exists polar night and midnight sun for coordinates beyond the polar circle. If the observer is standing directly on a pole, the sun is moving in circles around the pole:
Solar trajectories are obtained by plotting the solar elevation angle and azimuth in a spherical coordinate system:
Visualisation with Opengl:
https://www.youtube.com/watch?v=9oRLf2-qdus
Source code files:
The source code files are available at
github.






