Eine Gerade und ein Polygon sind im R3 gegeben. Die Gerade ist durch zwei Punkte definiert und gedanklich als Strahl definiert: Ein Punkt wo der Strahl hervorgeht und ein zweiter gibt die Richtung der Propagation vor. Das Polygon kann beliebig viele Punkt haben, mindestens aber drei. Alle Punkte des Polygons müssen in einer Ebene, welche beliebig ausgerichtet ist, liegen. Die Form des Polygons (konvex, konkav ... ) ist nicht relevant.
Die Frage ist: Wird der Strahl das Polygon treffen und wenn ja, wo ist dieser Punkt?
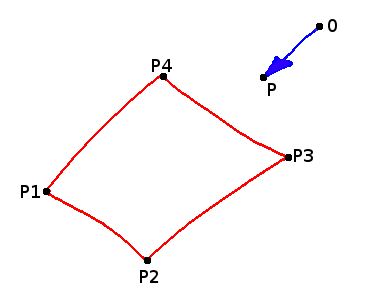
Folgendes muss gemacht werden, um diese Frage zu beantworten:
- 1. Berechne den Schnittpunkt zwischen dem Strahl und der Ebene in dem das Polygon liegt
- 2. Ausgehend von diesem Punkt wird ein neuer Strahl in Richtung des geometrischen Mittelpunktes des Polygons ausgesandt
- 3. Ermittle, wie oft dieser Strahl die Polygon-Umrandung schneidet
1. Berechne den Schnittpunkt zwischen dem Strahl und der Ebene in dem das Polygon liegt
Ebenengleichung:
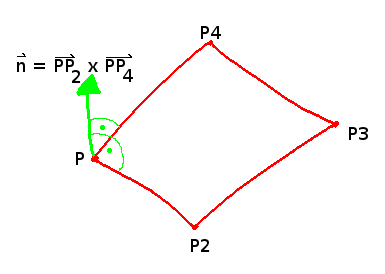
$$\color{red}{\big( \vec{p} - \vec{p_0} \big) \cdot \vec{n} = 0}$$
Geradengleichung:
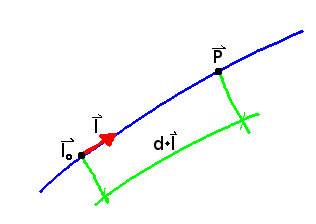
$$\color{blue}{\vec{p} = d \cdot \vec{l} + \vec{l_0} \hspace{1cm} d \in \mathbb{R}}$$
Einsetzen von der Geradengleichung in die Ebenengleichung:
$$\color{red}{\big[} \color{blue}{d \cdot \vec{l} + \vec{l_0}} \color{red}{- \vec{p_0} \big] \cdot \vec{n}= 0}$$
diese Gleichung nach \(d\) auflösen:
$$d = \frac{\vec{p_0} - \vec{l_0} \cdot \vec{n} }{\vec{l} \cdot \vec{n}} $$
Auf zwei Fälle muss hier aufgepasst werden:
\(\vec{l} \cdot \vec{n} = 0 \rightarrow \) die Gerade und die Ebene sind parallel
\( \big( \vec{p_0} - \vec{l_0} \big)\cdot \vec{n} = 0 \rightarrow \) die Gerade liegt in der Ebene
Mit Rücksicht auf die zwei Fälle oben können wir den Schnittpunkt berechnen:
$$ \vec{c_p} = d \cdot \vec{l} + \vec{l_0} = \underbrace{\frac{\vec{p_0} - \vec{l_0} \cdot \vec{n} }{\vec{l} \cdot \vec{n}}}_{d} \cdot \vec{l} + \vec{l_0} $$
2. Ausgehend von diesem Punkt wird ein neuer Strahl in Richtung des geometrischen Mittelpunktes des Polygons ausgesandt
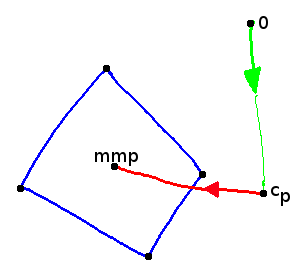
Der erste Schritt berechnet den Schnittpunkt der Ebene in der das Polygon liegt in der Geraden. Es bleibt noch zu prüfen, ob dieser Punkt in dem Polygon liegt oder nicht.
Die Idee ist, vom Punkt aus einen Strahl auszusenden und zu zählen, wie oft dieser Strahl die Grenzen des Polygons schneidet. Ist diese Zahl gerade, so befindet sich der Punkt außerhalb des Polygons. Bei einer ungeraden Anzahl von Schnitten befindet sich der Punkt innerhalb des Polygons (siehe Bild unten).
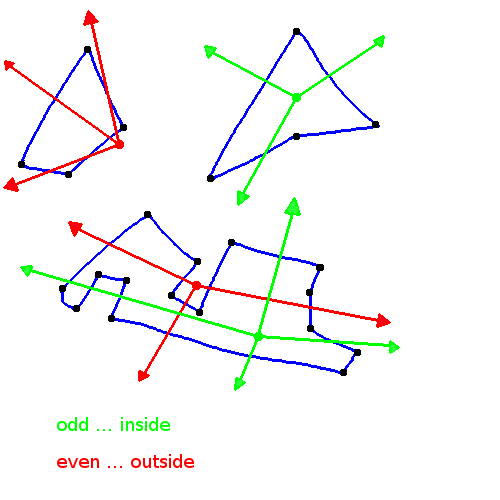
Die Richtung, in der wir den Strahl aussenden ist nicht relevant (genauso wie die Form des Polygons). Nachdem wir aber überhaupt keine Information über die Lage des Schnittpunktes haben, wählen wir als Richtung des Strahles den geometrischen Mittelpunkt des Polygons. So suchen wir immer in Richtung des Polygons.
3. Ermittle, wie oft dieser Strahl die Polygon-Umrandung schneidet
Jede Seite des Polygons wird nun auf Überschneidung getestet.
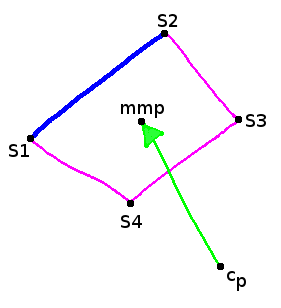
Die Liniengleichungen für die dargestellte Seite sind:
$$ \vec{x} = \vec{s_1} + t \cdot (\vec{s_2} - \vec{s_1}) $$
$$ \vec{x} = \vec{c_p} + s \cdot (\vec{mmp} - \vec{c_p}) $$
Gleichsetzen der beiden Gleichungen:
$$ \vec{s_1} + t \cdot (\vec{s_2} - \vec{s_1}) = \vec{c_p} + s \cdot (\vec{mmp} - \vec{c_p}) $$
Für jede Dimension (x/y/z) ausgeschrieben:
$$ s1.x + t \cdot (s2.x - s1.x) = c_p.x + s \cdot (mmp.x - c_p.x) $$
$$ s1.y + t \cdot (s2.y - s1.y) = c_p.y + s \cdot (mmp.y - c_p.y) $$
$$ s1.z + t \cdot (s2.z - s1.z) = c_p.z + s \cdot (mmp.z - c_p.z) $$
Zuerst extrahieren wir \( s \) von der ersten Gleichung:
$$ s = \frac{s1.x - c_p.x + t \cdot (s2.x - s1.x) }{ mmp.x - c_p.x} $$
und \( t \) von der zweiten:
$$ t = \frac{ c_p.y - s1.y + s \cdot (mmp.y - c_p.y) }{ s2.y - s1.y } $$
Dann setzen wir \( s \) in die zweite Gleichung:
$$ s1.y + t \cdot (s2.y - s1.y) = c_p.y + \underbrace{\frac{s1.x - c_p.x + t \cdot (s2.x - s1.x) }{ mmp.x - c_p.x}}_{s} \cdot (mmp.y - c_p.y) $$
Gleichung nach \( t \) auflösen:
$$ t = \frac{ -s1.y \cdot (mmp.x - c_p.x) + c_p.y \cdot (mmp.x - c_p.x) + s1.x \cdot (mmp.y - c_p.y) - c_p.x \cdot (mmp.y - c_p.y) }{ (s2.y - s1.y) \cdot (mmp.x - c_p.x) - (s2.x - s1.x) \cdot (mmp.y - c_p.y) } $$
Mit \( t \) kann auch der Parameter \( s \) bestimmt werden.
Zwei Anforderungen werden an \( t \) und \( s \) gestellt, damit der Schnittpunkt zählt:
- \( s > 0 \)
- \( 1 > t > 0 \)
Es sind nur Schnittpunkte relevant, welche in Strahlrichtung liegen (\( s > 0 \))
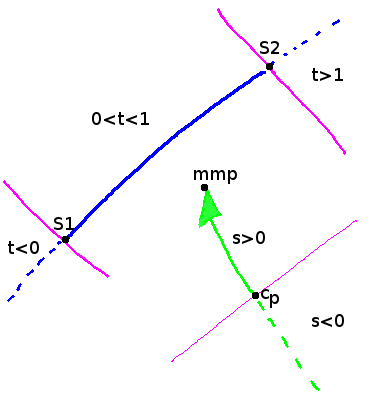
Zweitens muss der Parameter \( t \) Werte zwischen \( 0 \) und \( 1 \) annehmen damit der Strahl dieses Polygonteilstück schneidet (siehe Bild oben).
Das muss mit allen Teilen des Polygons gemacht werden und je nachdem ob die Summe dieser Schnittpunkte gerade oder ungerade ist wissen wir, ob der Punkt innerhalb oder außerhalb des Polygons liegt.
Ein kurzes Video dieses Teils:
https://www.youtube.com/watch?v=yL-DYzgwm6I
Der Punkt aus dem der Strahl hervorgeht ist rot dargestellt und die Propagationsrichtung türkis. Die vier Endpunkte des Polygons sind pink eingefärbt. Weiß dargestellt sind die jeweiligen Schnittpunkte und der geometrische Mittelpunkt des Polygons.
Die Linien-Linien-Schnitt-Tests am Ende können relativ einfach / eindeutig durchgeführt werden, da sich beide Linien in der selben Ebene befinden und wir daher
wissen, dass sich diese
eindeutig schneiden. Wenn dieses Wissen nicht vorhanden ist, dann ist diese Durchführung schwieriger.
Unten eine C++ Implementation:
ray_polygon_intersection()
Quellcode-Dateien:
https://github.com/clauskovacs/ray-polynom-intersection-3d
Ein kurzes Video einer Anwendung: Zehn vierseitige Rechtecke, welche zufällig um den Ursprung verteilt sind. Ein Strahl rotiert und es wird das erste Polygon ermittelt, welches der Strahl trifft und der Auftreffpunkt wird graphisch hervorgehoben:
https://www.youtube.com/watch?v=p_Gf65XAWso
