Let's assume that we have a polygon and a ray in 3d: The ray is defined by an origin, where it emanates and the direction of propagation (a total of two points) and the polygon is defined by (at least) three different points. Another assumption we make is, that all points of the polygon lie in the same plane. The polygon itself can have an arbitrary shape (convex, concave ... ) and location in space.
The question is: Will the ray intersect with the polygon and if so, where is the point of intersection.
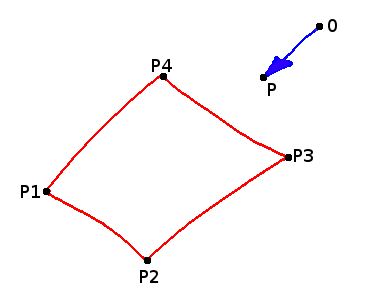
Following things will be done:
- 1. Calculate the point of intersection between the ray and the plane in which the polygon lies
- 2. Create a new ray from this point of intersection to the geometrical middel point of the polygon
- 3. Count how many times this new ray intersects with the polygon border lines
1. Calculate the point of intersection between the ray and the plane in which the polygon lies
equation of a plane:
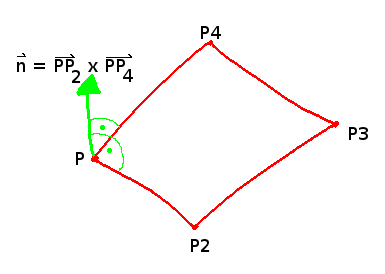
$$\color{red}{\big( \vec{p} - \vec{p_0} \big) \cdot \vec{n} = 0}$$
equation of a line:
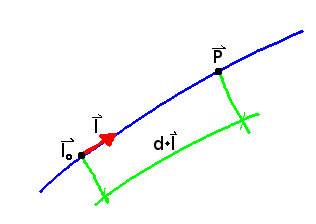
$$\color{blue}{\vec{p} = d \cdot \vec{l} + \vec{l_0} \hspace{1cm} d \in \mathbb{R}}$$
Inserting the line-equation into the plane-equation yields:
$$\color{red}{\big[} \color{blue}{d \cdot \vec{l} + \vec{l_0}} \color{red}{- \vec{p_0} \big] \cdot \vec{n}= 0}$$
solving the equation for \(d\):
$$d = \frac{\vec{p_0} - \vec{l_0} \cdot \vec{n} }{\vec{l} \cdot \vec{n}} $$
Two cases need to be checked:
\(\vec{l} \cdot \vec{n} = 0 \rightarrow \) the ray and the plane are parallel
\( \big( \vec{p_0} - \vec{l_0} \big)\cdot \vec{n} = 0 \rightarrow \) the ray lies in the plane
With regard to the two cases above, we can calulate the point of intersection using:
$$ \vec{c_p} = d \cdot \vec{l} + \vec{l_0} = \underbrace{\frac{\vec{p_0} - \vec{l_0} \cdot \vec{n} }{\vec{l} \cdot \vec{n}}}_{d} \cdot \vec{l} + \vec{l_0} $$
2. Create a new ray from this point of intersection to the geometrical middel point of the polygon
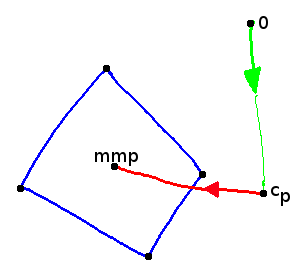
From the first step, we obtained the point of intersection between the ray and the plane in which the polygon lies. The question now is, whether this point lies inside of the polygon or not.
The idea is, to cast a ray from the point we want to check (if it lies inside of the polygon) and count how many times this ray crossed a border lines of the polygon. If the amount is odd, the point is inside of the polygon. If it's even then the point resides outside of the polygon.
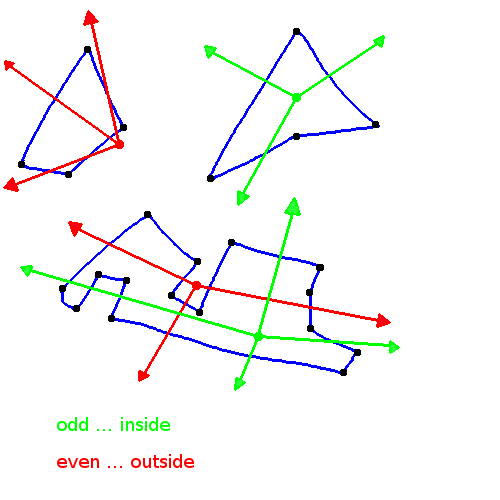
The direction the ray is cast to can be chosen completely arbitrary.Since the point of intersection between the initial ray and the plane can be anywhere (inside and outside of the polygon) the ray should be pointing towards the polygon. We ensure this with propagating the ray towards the geometrical middle point of the ray. This way the direction is always towards the polygon.
3. Count how many times this new ray intersects with the polygon border lines
Illustrated for one side of the polygon (\( \vec{s_1} \rightarrow \vec{s_2} \)) and the ray being cast from the point of collision \( \vec{c_p} \) to the geometrical middle point of the polygon \( \vec{mmp} \).
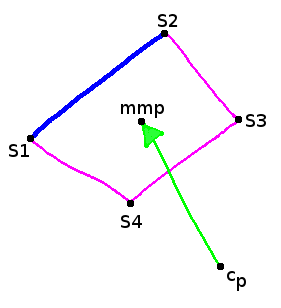
The linear equations are:
$$ \vec{x} = \vec{s_1} + t \cdot (\vec{s_2} - \vec{s_1}) $$
$$ \vec{x} = \vec{c_p} + s \cdot (\vec{mmp} - \vec{c_p}) $$
Equalizing the two equations:
$$ \vec{s_1} + t \cdot (\vec{s_2} - \vec{s_1}) = \vec{c_p} + s \cdot (\vec{mmp} - \vec{c_p}) $$
One equation for each dimension:
$$ s1.x + t \cdot (s2.x - s1.x) = c_p.x + s \cdot (mmp.x - c_p.x) $$
$$ s1.y + t \cdot (s2.y - s1.y) = c_p.y + s \cdot (mmp.y - c_p.y) $$
$$ s1.z + t \cdot (s2.z - s1.z) = c_p.z + s \cdot (mmp.z - c_p.z) $$
First we extract \( s \) from the first equation:
$$ s = \frac{s1.x - c_p.x + t \cdot (s2.x - s1.x) }{ mmp.x - c_p.x} $$
and \( t \) from the second:
$$ t = \frac{ c_p.y - s1.y + s \cdot (mmp.y - c_p.y) }{ s2.y - s1.y } $$
Then we insert the extracted \( s \) into the second equation:
$$ s1.y + t \cdot (s2.y - s1.y) = c_p.y + \underbrace{\frac{s1.x - c_p.x + t \cdot (s2.x - s1.x) }{ mmp.x - c_p.x}}_{s} \cdot (mmp.y - c_p.y) $$
Solve the equation above for \( t \):
$$ t = \frac{ -s1.y \cdot (mmp.x - c_p.x) + c_p.y \cdot (mmp.x - c_p.x) + s1.x \cdot (mmp.y - c_p.y) - c_p.x \cdot (mmp.y - c_p.y) }{ (s2.y - s1.y) \cdot (mmp.x - c_p.x) - (s2.x - s1.x) \cdot (mmp.y - c_p.y) } $$
With \( t \) it's easy to calculate the parameter \( s \).
Two requirements must be met so that the ray crosses this line segment:
- \( s > 0 \)
- \( 1 > t > 0 \)
We are only interested in points of intersections in the direction of the ray (\( s > 0 \)).
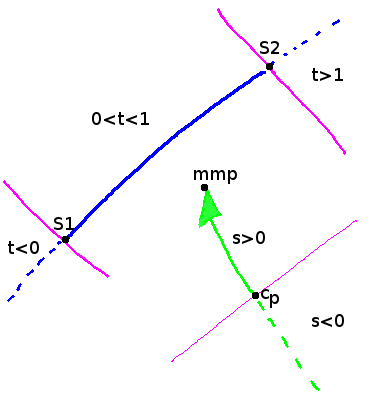
Secondly, the parameter \( t \) must have a value between \( 0 \) and \( 1 \) or else the ray misses the side of the polygon.
After doing this intersection check for all border elements of the polygon and counting the amount of intersections, we know whether the point lies inside of the polygon or not.
A short video demonstrating this part:
https://www.youtube.com/watch?v=yL-DYzgwm6I
The point where the ray emerges is colored red and the point where it propagates turquoise. The four endpoints of the polygon (pink) and the geometrical middle point and the points of intersection are drawn white.
The last line-intersection-tests are quite easy because we know that both lines are element of the same plane and therefore
must intersect. If we don't know this, the determination of collision becomes more complicated.
Below a C++ implementation:
ray_polygon_intersection()
Source code files:
https://github.com/clauskovacs/ray-polynom-intersection-3d
Below another short video: Ten 4-sided squares are scattered randomly around the origin. A ray rotates around an axis and the closest point of intersection is drawn as well as the polygon which intersects firstly with the ray.
https://www.youtube.com/watch?v=p_Gf65XAWso



 $$\color{red}{\big( \vec{p} - \vec{p_0} \big) \cdot \vec{n} = 0}$$
equation of a line:
$$\color{red}{\big( \vec{p} - \vec{p_0} \big) \cdot \vec{n} = 0}$$
equation of a line:
 $$\color{blue}{\vec{p} = d \cdot \vec{l} + \vec{l_0} \hspace{1cm} d \in \mathbb{R}}$$
Inserting the line-equation into the plane-equation yields:
$$\color{red}{\big[} \color{blue}{d \cdot \vec{l} + \vec{l_0}} \color{red}{- \vec{p_0} \big] \cdot \vec{n}= 0}$$
solving the equation for \(d\):
$$d = \frac{\vec{p_0} - \vec{l_0} \cdot \vec{n} }{\vec{l} \cdot \vec{n}} $$
Two cases need to be checked:
$$\color{blue}{\vec{p} = d \cdot \vec{l} + \vec{l_0} \hspace{1cm} d \in \mathbb{R}}$$
Inserting the line-equation into the plane-equation yields:
$$\color{red}{\big[} \color{blue}{d \cdot \vec{l} + \vec{l_0}} \color{red}{- \vec{p_0} \big] \cdot \vec{n}= 0}$$
solving the equation for \(d\):
$$d = \frac{\vec{p_0} - \vec{l_0} \cdot \vec{n} }{\vec{l} \cdot \vec{n}} $$
Two cases need to be checked:

 The direction the ray is cast to can be chosen completely arbitrary.Since the point of intersection between the initial ray and the plane can be anywhere (inside and outside of the polygon) the ray should be pointing towards the polygon. We ensure this with propagating the ray towards the geometrical middle point of the ray. This way the direction is always towards the polygon.
The direction the ray is cast to can be chosen completely arbitrary.Since the point of intersection between the initial ray and the plane can be anywhere (inside and outside of the polygon) the ray should be pointing towards the polygon. We ensure this with propagating the ray towards the geometrical middle point of the ray. This way the direction is always towards the polygon.
 The linear equations are:
The linear equations are:
 Secondly, the parameter \( t \) must have a value between \( 0 \) and \( 1 \) or else the ray misses the side of the polygon.
Secondly, the parameter \( t \) must have a value between \( 0 \) and \( 1 \) or else the ray misses the side of the polygon.